Category Encodersのすゝめ【AI道場「Kaggle」への道 by 日経 xTECH ビジネスAI① Advent Calendar 2019 10日目】

こんにちは！たかぱい（@takapy0210）です。

本記事は、AI道場「Kaggle」への道 by 日経 xTECH ビジネスAI① Advent Calendar 2019の10日目の記事です。

今回は、最近よく使用しているCategory Encodersを動かしてみた結果をまとめてみようと思います。

Category Encodersとは

カテゴリ変数をさまざまな数値変数に変換してくれるライブラリです。

One-Hot EncodingやOrdinal（Label） Encodingなどの定番の変換手法はもちろん、Target EncodingといったKaggleなどの分析コンペでもよく使われている手法が多く収録されており、個人的にオススメのライブラリです。

このCategory Encodersはscikit-learn-contribプロジェクトの1つに登録されおり、scikit-learnのAPIの流儀に従って実装されているため、scikit-learnに親しい人であれば違和感なく使えるのも1つの特徴だと思います。

公式ドキュメント：
contrib.scikit-learn.org

ドキュメントを見ていただくと分かると思いますが、冒頭で挙げた有名どころの他にも多くのContentsを含んでいます。 本日はこれらを用いたらどのような変換をしてくれるのかを検証していければと思います。

※実際のモデルへ適用し精度の検証までは行っていません。今回はあくまでどのような動作をするのかを検証してみたものになります。

（余談）なぜカテゴリ変数は変換が必要なのか

機械学習において特徴量を生成しモデルを学習させる際、多くのアルゴリズムではカテゴリカルな変数（e.g. 地域・天気・血液型・所属組織）は、そのままの形（数値で表現されていない形）では学習させることができません。
そこで、何らかの量的変数に置き換えて表現する必要があります。

このようにカテゴリカル変数→量的変数に変換してくれるライブラリの1つが今回紹介するCategory Encodersです。

使用するデータ

今回検証に使用したデータはfeaturetoolsから取得したデモデータです。
検証するために意図的にデータを整形しています。

import featuretools as ft
import numpy as np
import pandas as pd

data = ft.demo.load_mock_customer()
df = data['sessions']
df = df[['customer_id', 'device']].head(12)
df[7:8]['device'] = 'laptop'

# Target Encodingの検証用にカラムを追加
np.random.seed(seed=3)
df['target'] = np.random.randint(1, 10, size=len(df))

これで下記のようなデータフレームが生成されます。
今回はこのdeviceカラムをゴニョゴニョしていきます。

• df

customer_id	device	target
2	desktop	9
5	mobile	4
4	mobile	9
1	mobile	9
4	mobile	1
1	tablet	6
3	tablet	4
4	laptop	6
1	desktop	8
2	tablet	7
4	mobile	1
4	desktop	5

また、コンペで利用することも想定し、下記のようにtrainとtestも作っておきます。

コンペや実務でも遭遇するパターンとして、laptopに関してはtestデータにのみ存在する水準としています。

train = df[:7]
test = df[7:]

• train

customer_id	device	target
2	desktop	9
5	mobile	4
4	mobile	9
1	mobile	9
4	mobile	1
1	tablet	6
3	tablet	4

• test

customer_id	device	target
4	laptop	6
1	desktop	8
2	tablet	7
4	mobile	1
4	desktop	5

前提

Category EncodingとTarget Encodingに分けて紹介していきます。

どちらもカテゴリ変数の変換ですが、下記のようにEncode時に必要な引数が異なるため、敢えて分けて記載します。

• Category Encoding：Encodeに目的変数を必要としない
• Target Encoding：Encodeに目的変数を必要とする

準備

pipでインストールできます。

pip install category_encoders

また、下記のようにimportしてカラムを指定しておきます。

import category_encoders as ce
cate_col = 'device'
target_col= 'target'

Category Encoding

One Hot

おなじみのやつです。

これまた余談ですが、sklearn.preprocessingでOne-Hot Encodingなどをやろうとすと結構辛かったりします。
（numpyで返ってくるので、それをまたDataFrameに変換しないといけない・・・とk）

その点、category_encoders使えば下記のようにシンプルに記述できます。

ohe = ce.OneHotEncoder(cols=cate_col, drop_invariant=True)
ohe_df = ohe.fit_transform(df[cate_col])
pd.concat([df[cate_col], ohe_df], axis=1)

device	device_1	device_2	device_3	device_4
desktop	1	0	0	0
mobile	0	1	0	0
mobile	0	1	0	0
mobile	0	1	0	0
mobile	0	1	0	0
tablet	0	0	1	0
tablet	0	0	1	0
laptop	0	0	0	1
desktop	1	0	0	0
tablet	0	0	1	0
mobile	0	1	0	0
desktop	1	0	0	0

Ordinal

これはkagglerの間で言われるLabel Encodingと同じやつです。

oe = ce.OrdinalEncoder(cols=cate_col, drop_invariant=True)
oe_df = oe.fit_transform(df[cate_col])
pd.concat([df[cate_col], oe_df], axis=1)

device	device
desktop	1
mobile	2
mobile	2
mobile	2
mobile	2
tablet	3
tablet	3
laptop	4
desktop	1
tablet	3
mobile	2
desktop	1

Binary

カテゴリをバイナリビット文字列に変換してくれます。

be = ce.BinaryEncoder(cols=cate_col, drop_invariant=True)
be_df = be.fit_transform(df[cate_col])
pd.concat([df[cate_col], be_df], axis=1)

device	device_0	device_1	device_2
desktop	0	0	1
mobile	0	1	0
mobile	0	1	0
mobile	0	1	0
mobile	0	1	0
tablet	0	1	1
tablet	0	1	1
laptop	1	0	0
desktop	0	0	1
tablet	0	1	1
mobile	0	1	0
desktop	0	0	1

BaseN

BaseNはbaseオプションに指定する値によって、One-Hot / Binary / Ordinal Encodingを使い分けることができます。

base = 1

bne = ce.BaseNEncoder(cols=cate_col, base=1, drop_invariant=True)
bne_df = bne.fit_transform(df[cate_col])
pd.concat([df[cate_col], bne_df], axis=1)

device	device_1	device_2	device_3	device_4
desktop	1	0	0	0
mobile	0	1	0	0
mobile	0	1	0	0
mobile	0	1	0	0
mobile	0	1	0	0
tablet	0	0	1	0
tablet	0	0	1	0
laptop	0	0	0	1
desktop	1	0	0	0
tablet	0	0	1	0
mobile	0	1	0	0
desktop	1	0	0	0

One-Hot Encodingと同様の結果が得られます。

base = 5

bne = ce.BaseNEncoder(cols=cate_col, base=5, drop_invariant=True)
bne_df = bne.fit_transform(df[cate_col])
pd.concat([df[cate_col], bne_df], axis=1)

device	device_1
desktop	1
mobile	2
mobile	2
mobile	2
mobile	2
tablet	3
tablet	3
laptop	4
desktop	1
tablet	3
mobile	2
desktop	1

baseの値を水準数 + 1に設定するとOdinal Encodingと同様の結果が得られます。

Hashing

One-Hot Encodingでの変換において、特徴量の数はカテゴリの水準数と等しくなりますが、Feature Hashingを用いることでその数を少なくすることが可能です。
水準数を少なくしているので、ハッシュ関数の計算によっては異なる水準でも同じ場所にフラグが立つことがあります。

カテゴリの水準数が多く、One-Hot Encodingを行うと特徴量が膨大になってしまう場合に利用することが多いです。
（が、主流アルゴリズムがGBDTとなっている今では、One-HotやHashingを用いずに、Ordinal Encodingを使用することが多いと思います）

Hashingはn_componentsで変換後の特徴量の数を決定することができます。（省略時デフォルトは8）

he = ce.HashingEncoder(cols=cate_col)
he_df = he.fit_transform(df[cate_col])
pd.concat([df[cate_col], he_df], axis=1)

device	col_0	col_1	col_2	col_3	col_4	col_5	col_6	col_7
desktop	0	0	0	0	0	1	0	0
mobile	1	0	0	0	0	0	0	0
mobile	1	0	0	0	0	0	0	0
mobile	1	0	0	0	0	0	0	0
mobile	1	0	0	0	0	0	0	0
tablet	0	0	0	0	0	1	0	0
tablet	0	0	0	0	0	1	0	0
laptop	0	0	0	0	1	0	0	0
desktop	0	0	0	0	0	1	0	0
tablet	0	0	0	0	0	1	0	0
mobile	1	0	0	0	0	0	0	0
desktop	0	0	0	0	0	1	0	0

このままだと、全てが0のカラムも返ってきてしまうので、drop_invariant=Trueとすると、1が設定されているカラムのみを取得することができます。

he = ce.HashingEncoder(cols=cate_col, drop_invariant=True)
he_df = he.fit_transform(df[cate_col])
pd.concat([df[cate_col], he_df], axis=1)

device	col_0	col_4	col_5
desktop	0	0	1
mobile	1	0	0
mobile	1	0	0
mobile	1	0	0
mobile	1	0	0
tablet	0	0	1
tablet	0	0	1
laptop	0	1	0
desktop	0	0	1
tablet	0	0	1
mobile	1	0	0
desktop	0	0	1

Backward Difference Coding

下記のように変換されます。

Backward Difference Codingの例（k = 4）

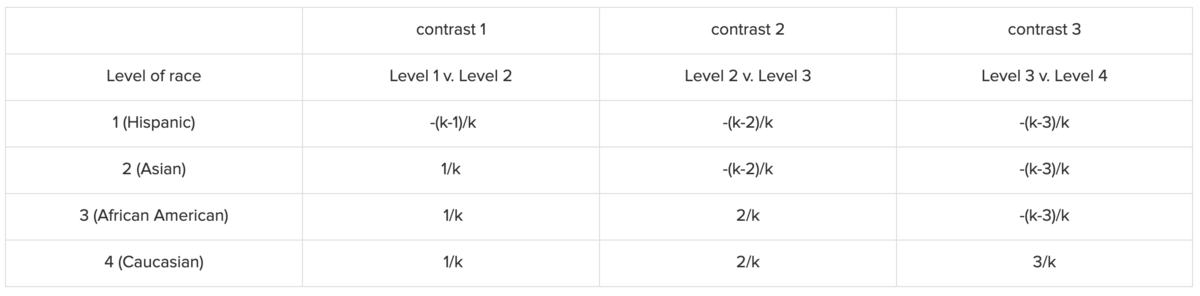
詳細はこちらを参照。

This type of coding may be useful with either a nominal or an ordinal variable.

と記載があるので、名義尺度または順序尺度の変数の変換に向いていると思われます。

bdc = ce.BackwardDifferenceEncoder(cols=cate_col, drop_invariant=True)
bdc_df = bdc.fit_transform(df[cate_col])
pd.concat([df[cate_col], bdc_df], axis=1)

device	device_0	device_1	device_2
desktop	-0.75	-0.5	-0.25
mobile	0.25	-0.5	-0.25
mobile	0.25	-0.5	-0.25
mobile	0.25	-0.5	-0.25
mobile	0.25	-0.5	-0.25
tablet	0.25	0.5	-0.25
tablet	0.25	0.5	-0.25
laptop	0.25	0.5	0.75
desktop	-0.75	-0.5	-0.25
tablet	0.25	0.5	-0.25
mobile	0.25	-0.5	-0.25
desktop	-0.75	-0.5	-0.25

Helmert Coding

下記のように変換されます。

Helmert Codingの例（k=4）

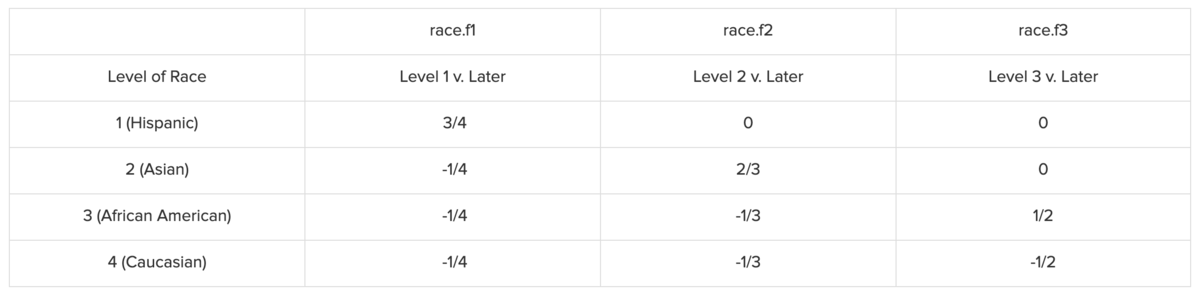
詳細はこちらを参照。

hme = ce.HelmertEncoder(cols=cate_col, drop_invariant=True)
hme_df = hme.fit_transform(df[cate_col])
pd.concat([df[cate_col], hme_df], axis=1)

device	device_0	device_1	device_2
desktop	-1	-1	-1
mobile	1	-1	-1
mobile	1	-1	-1
mobile	1	-1	-1
mobile	1	-1	-1
tablet	0	2	-1
tablet	0	2	-1
laptop	0	0	3
desktop	-1	-1	-1
tablet	0	2	-1
mobile	1	-1	-1
desktop	-1	-1	-1

Polynomial Coding

下記のように変換されます。

Polynomial Codingの例（k=4）

This type of coding system should be used only with an ordinal variable in which the levels are equally spaced.

と記載があるので、順序尺度の変数の変換に向いていると思われます。

詳細はこちらを参照。

pe = ce.PolynomialEncoder(cols=cate_col, drop_invariant=True)
pe_df = pe.fit_transform(df[cate_col])
pd.concat([df[cate_col], pe_df], axis=1)

device	device_0	device_1	device_2
desktop	-0.6708	0.5000	-0.2236
mobile	-0.2236	-0.5000	0.6708
mobile	-0.2236	-0.5000	0.6708
mobile	-0.2236	-0.5000	0.6708
mobile	-0.2236	-0.5000	0.6708
tablet	0.2236	-0.5000	-0.6708
tablet	0.2236	-0.5000	-0.6708
laptop	0.6708	0.5000	0.2236
desktop	-0.6708	0.5000	-0.2236
tablet	0.2236	-0.5000	-0.6708
mobile	-0.2236	-0.5000	0.6708
desktop	-0.6708	0.5000	-0.2236

Sum Coding

下記のように1つの水準を全て-1で表現し、残りはOne-Hotで表現します。（Effect Codingと同じっぽい？）

Sum Codingの例（k=4）

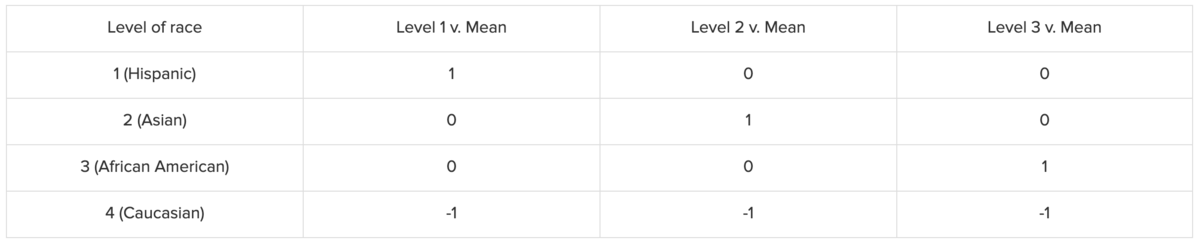
詳細はこちらを参照。

se = ce.SumEncoder(cols=cate_col, drop_invariant=True)
se_df = se.fit_transform(df[cate_col])
pd.concat([df[cate_col], se_df], axis=1)

device	device_0	device_1	device_2
desktop	1	0	0
mobile	0	1	0
mobile	0	1	0
mobile	0	1	0
mobile	0	1	0
tablet	0	0	1
tablet	0	0	1
laptop	-1	-1	-1
desktop	1	0	0
tablet	0	0	1
mobile	0	1	0
desktop	1	0	0

Target Encoding

Target Encodingとは、目的変数を用いてカテゴリ変数を数値に変換する手法です。
目的変数をリークさせる可能性があるので、使うときには注意が必要です。
（リークさせないためには、自身の目的変数の値をEncodingに使用しない、などが挙げられます）

Target Encoder

For the case of categorical target: features are replaced with a blend of posterior probability of the target given particular categorical value and the prior probability of the target over all the training data.

のように、回帰と分類でアプローチの方法が異なるようですが深ぼって検証はできていません。（のでそのうちやります）

te = ce.TargetEncoder(cols=cate_col)
te_train = te.fit_transform(train[cate_col], train[target_col])
te_test = te.transform(test[cate_col])

train_df = pd.concat([train[[cate_col, target_col]], te_train], axis=1)
test_df = pd.concat([test[[cate_col, target_col]], te_test], axis=1)

• train_df

device	target	device
desktop	9	6.000
mobile	4	5.762
mobile	9	5.762
mobile	9	5.762
mobile	1	5.762
tablet	6	5.269
tablet	4	5.269

• test_df

device	target	device
laptop	6	6.000
desktop	8	6.000
tablet	7	5.269
mobile	1	5.762
desktop	5	6.000

Leave One Out

自分自身を除いた値を用いてTarget Encodingしてくれる手法です。

loo = ce.LeaveOneOutEncoder(cols=cate_col)
loo_train = loo.fit_transform(train[cate_col], train[target_col])
loo_test = loo.transform(test[cate_col])

train_df = pd.concat([train[[cate_col, target_col]], loo_train], axis=1)
test_df = pd.concat([test[[cate_col, target_col]], loo_test], axis=1)

• train_df

device	target	device
desktop	9	6.000
mobile	4	6.333
mobile	9	4.667
mobile	9	4.667
mobile	1	7.333
tablet	6	4.000
tablet	4	6.000

• test_df

device	target	device
laptop	6	6.00
desktop	8	6.00
tablet	7	5.00
mobile	1	5.75
desktop	5	6.00

このEncodingですが、下記のようにfitとtransformを別で実行すると値が変化するので注意が必要です。

loo = ce.LeaveOneOutEncoder(cols=cate_col).fit(train[cate_col], train[target_col])
loo_train = loo.transform(train[cate_col])
loo_test = loo.transform(test[cate_col])

train_df = pd.concat([train[[cate_col, target_col]], loo_train], axis=1)
test_df = pd.concat([test[[cate_col, target_col]], loo_test], axis=1)

• train_df

device	target	device
desktop	9	6.00
mobile	4	5.75
mobile	9	5.75
mobile	9	5.75
mobile	1	5.75
tablet	6	5.00
tablet	4	5.00

• test_df

device	target	device
laptop	6	6.00
desktop	8	6.00
tablet	7	5.00
mobile	1	5.75
desktop	5	6.00

fitとtransformを別で実行するとTarget Encoderに近い変換になります。

CatBoost Encoder

CatBoostの内部での変換を真似してやってしまおう、というもの（？）みたいです。 このリファレンスのいずれかの式で算出していると思うのですが、正確なところまでは分かりませんでした。（ソースコードを見れば分かるとは思います）

cbe = ce.CatBoostEncoder(cols=cate_col, random_state=42)
cbe_train = cbe.fit_transform(train[cate_col], train[target_col])
cbe_test = cbe.transform(test[cate_col])

train_df = pd.concat([train[[cate_col, target_col]], cbe_train], axis=1)
test_df = pd.concat([test[[cate_col, target_col]], cbe_test], axis=1)

• train_df

device	target	device
desktop	9	6.00
mobile	4	6.00
mobile	9	5.00
mobile	9	6.33
mobile	1	7.00
tablet	6	6.00
tablet	4	6.00

• test_df

device	target	device
laptop	6	6.00
desktop	8	6.00
tablet	7	5.33
mobile	1	5.80
desktop	5	6.00

James-Stein Encoder

James-Stein推定量を使用しているみたい。（この辺りは知識不足で分からず。勉強します）

ドキュメントには下記の加重平均を用いていると記載されています。

1. 観測された特徴量の目的変数の平均値
2. 全ての目的変数の平均値

jse = ce.JamesSteinEncoder(cols=cate_col, drop_invariant=True)
jse_train = jse.fit_transform(train[cate_col], train[target_col])
jse_test = jse.transform(test[cate_col])

train_df = pd.concat([train[[cate_col, target_col]], jse_train], axis=1)
test_df = pd.concat([test[[cate_col, target_col]], jse_test], axis=1)

• train_df

device	target	device
desktop	9	9.00
mobile	4	5.75
mobile	9	5.75
mobile	9	5.75
mobile	1	5.75
tablet	6	5.00
tablet	4	5.00

• test_df

device	target	device
laptop	6	6.00
desktop	8	9.00
tablet	7	5.00
mobile	1	5.75
desktop	5	9.00

M-estimate

Target Encoderをよりシンプルにしたもの、という記載がされている。 mの値が大きいほど、収縮が強くなる。

m = 1.0

ms = ce.MEstimateEncoder(cols=cate_col, m=1.0)
ms_train = ms.fit_transform(train[cate_col], train[target_col])
ms_test = ms.transform(test[cate_col])

train_df = pd.concat([train[[cate_col, target_col]], ms_train], axis=1)
test_df = pd.concat([test[[cate_col, target_col]], ms_test], axis=1)

• train_df

device	target	device
desktop	9	7.500
mobile	4	5.800
mobile	9	5.800
mobile	9	5.800
mobile	1	5.800
tablet	6	5.333
tablet	4	5.333

• test_df

device	target	device
laptop	6	6.000
desktop	8	7.500
tablet	7	5.333
mobile	1	5.800
desktop	5	7.500

m = 0.01

ms = ce.MEstimateEncoder(cols=cate_col, m=0.01)
ms_train = ms.fit_transform(train[cate_col], train[target_col])
ms_test = ms.transform(test[cate_col])

train_df = pd.concat([train[[cate_col, target_col]], ms_train], axis=1)
test_df = pd.concat([test[[cate_col, target_col]], ms_test], axis=1)

• train_df

device	target	device
desktop	9	8.970
mobile	4	5.751
mobile	9	5.751
mobile	9	5.751
mobile	1	5.751
tablet	6	5.005
tablet	4	5.005

• test_df

device	target	device
laptop	6	6.000
desktop	8	8.727
tablet	7	5.048
mobile	1	5.756
desktop	5	8.727

たしかに、mが大きい方が数値の分散が少なくなっていることが分かる。

Weight of Evidence

Weight of Evidence (WOE) helps to transform a continuous independent variable into a set of groups or bins based on similarity of dependent variable distribution

と記載があるので、連続した量的データに対して有効のようです。

詳細はこちらを参照。

また、これは目的変数がbinary（2値分類）の必要があるため、targetを以下のように変更します。

np.random.seed(seed=3)
train['target'] = np.random.randint(0, 2, size=len(train))
test['target'] = np.random.randint(0, 2, size=len(test))

• train

customer_id	device	target
2	desktop	0
5	mobile	0
4	mobile	1
1	mobile	1
4	mobile	0
1	tablet	0
3	tablet	0

• test

customer_id	device	target
4	laptop	1
1	desktop	1
2	tablet	1
4	mobile	0
4	desktop	1

この状態で変換してみます。

woe = ce.WOEEncoder(cols=cate_col)
woe_train = woe.fit_transform(train[cate_col], train[target_col])
woe_test = woe.transform(test[cate_col])

train_df  = pd.concat([train[[cate_col, target_col]], woe_train], axis=1)
test_df = pd.concat([test[[cate_col, target_col]], woe_test], axis=1)

• train_df

device	target	device
desktop	0	0.0000
mobile	0	0.5596
mobile	1	0.5596
mobile	1	0.5596
mobile	0	0.5596
tablet	0	-0.5390
tablet	0	-0.5390

• test_df

device	target	device
laptop	1	0.000
desktop	1	0.000
tablet	1	-0.539
mobile	0	0.560
desktop	1	0.000

最後に

いかがでしたでしょうか。
（書き始めたのが当日の0時過ぎだったこともあり、深いところまで調査できずに終わってしまいました。準備が大切ですね）

自分でも知らない変換手法が多くあり、とても勉強になりました。（検証したみたけど内部でどのような計算をしているかまだ分かっていないものもありますので、この辺りもコードを読んでみようと思います）

また、今まではsklearnなどを使ってオレオレ関数を作って実装していましたが、Category Encodersを使用することで、よりシンプルに実装できているので、「カテゴリ変換どうにかなんね〜かなぁ」と悩んでいる方は是非一度使ってみてはいかがでしょうか。

次は各種変換方法でカテゴリを変換したもので実際にモデリングして、scoreへの影響などを調査できればと思っています。