前回に引き続き、4章で学んだことを残しておきます。
今回は、MNISTデータセットを使用して、手書き数字を学習するニューラルネットワークを構築してみます。
前回までの記事はこちら
taxa-program.hatenablog.com
taxa-program.hatenablog.com
2層ニューラルネットワークのクラス
はじめに、2層ニューラルネットワークを一つのクラスとして実装してみます。
処理の内容は、なるべくコメントに記載しています。(したつもりでいます)
誤っている部分がある場合はご指摘いただけると助かります。
少し補足すると、params変数には、このネットワークに必要な全ての重みパラメータが格納されています。
また、grads変数には、params変数と対応するように、各パラメータの勾配が格納されています。
mine_two_layer_net.py
# coding: utf-8 import sys, os sys.path.append(os.pardir) from common.functions import * from common.gradient import numerical_gradient # 勾配を求める関数 class TwoLayerNet: # コンストラクタ # 引数は(入力層のニューロン数, 隠れ層のニューロン数, 出力層のニューロン数) def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01): # 重みの初期化 self.params = {} # 辞書型で初期化 self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size) # ガウス分布で input_size * hidden_size の配列生成 self.params['b1'] = np.zeros(hidden_size) self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size) # 予測 def predict(self, x): # 重み、バイアスの設定 W1, W2 = self.params['W1'], self.params['W2'] b1, b2 = self.params['b1'], self.params['b2'] # y = (w1*入力値1 + b1) + w2*入力値2(1層目からの出力値) + b2 a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) # 活性化関数(シグモイド関数)を使用して、入力信号を出力信号へ変換 a2 = np.dot(z1, W2) + b2 y = softmax(a2) # ソフトマックス関数を利用して、確率を出力 return y # 損失関数(交差エントロピー)を求める def loss(self, x, t): # 予測値yハット y = self.predict(x) # 予測値yハットと、教師データtの損失関数の値を取得 return cross_entropy_error(y, t) # 認識精度を求める def accuracy(self, x, t): # 予測値yハット y = self.predict(x) # 配列の中で最大の要素のインデックスを取得 y = np.argmax(y, axis=1) t = np.argmax(t, axis=1) # 認識精度の計算 # 予測値 = 正解値の合計 / 全データ数 accuracy = np.sum(y == t) / float(x.shape[0]) return accuracy # 勾配を求める # x:入力データ, t:教師データ def numerical_gradient(self, x, t): loss_W = lambda W: self.loss(x, t) # 勾配を保持 grads = {} grads['W1'] = numerical_gradient(loss_W, self.params['W1']) # 1層目の重みの勾配 grads['b1'] = numerical_gradient(loss_W, self.params['b1']) # 1層目のバイアスの勾配 grads['W2'] = numerical_gradient(loss_W, self.params['W2']) # 2層目の重みの勾配 grads['b2'] = numerical_gradient(loss_W, self.params['b2']) # 2層目のバイアスの勾配 return grads # 勾配を求める(高速版) def gradient(self, x, t): W1, W2 = self.params['W1'], self.params['W2'] b1, b2 = self.params['b1'], self.params['b2'] grads = {} batch_num = x.shape[0] # forward a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 y = softmax(a2) # backward dy = (y - t) / batch_num grads['W2'] = np.dot(z1.T, dy) grads['b2'] = np.sum(dy, axis=0) da1 = np.dot(dy, W2.T) dz1 = sigmoid_grad(a1) * da1 grads['W1'] = np.dot(x.T, dz1) grads['b1'] = np.sum(dz1, axis=0) return grads
ミニバッチ学習の実装と評価
前セクションで、ニューラルネットワークの構築クラスは作成済みなので、
このセクションでは、ミニバッチ処理での学習とテストデータでの評価方法をまとめます。
mine_train_neuralnet.py
# coding: utf-8 # ミニバッチ処理での学習とテストデータでの評価 import sys, os sys.path.append(os.pardir) import numpy as np import matplotlib.pyplot as plt from dataset.mnist import load_mnist from mine_two_layer_net import TwoLayerNet # データの読み込み (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True) train_loss_list = [] train_acc_list = [] test_acc_list = [] # ハイパーパラメータの設定 iters_num = 5000 # 繰り返しの回数を任意設定 train_size = x_train.shape[0] batch_size = 100 learning_rate = 0.1 # 1エポックあたりの繰り返し数 iter_per_epoch = max(train_size / batch_size, 1) # 2層のニューラルネットワークを構築 network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10) for i in range(iters_num): # ミニバッチの取得 batch_mask = np.random.choice(train_size, batch_size) # 無作為に100データを抽出 x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 勾配の計算 # grad = network.numerical_gradient(x_batch, t_batch) grad = network.gradient(x_batch, t_batch) #高速版 # パラメータの更新 for key in ('W1', 'b1', 'W2', 'b2'): network.params[key] -= learning_rate * grad[key] # 学習過程の記録 loss = network.loss(x_batch, t_batch) train_loss_list.append(loss) # 訓練データの1エポック毎の認識精度を記録し表示する if i % iter_per_epoch == 0: train_acc = network.accuracy(x_train, t_train) test_acc = network.accuracy(x_test, t_test) train_acc_list.append(train_acc) test_acc_list.append(test_acc) print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc)) # グラフの描画 markers = {'train': 'o', 'test': 's'} x = np.arange(len(train_acc_list)) plt.plot(x, train_acc_list, label='train acc') plt.plot(x, test_acc_list, label='test acc', linestyle='--') plt.xlabel("epochs") plt.ylabel("accuracy") plt.ylim(0, 1.0) plt.legend(loc='lower right') plt.show()
結果は、
train acc, test acc | 0.09736666666666667, 0.0982 train acc, test acc | 0.77655, 0.7832 train acc, test acc | 0.8754333333333333, 0.8803 train acc, test acc | 0.8972, 0.9006 train acc, test acc | 0.9065833333333333, 0.9095 train acc, test acc | 0.9131333333333334, 0.9146 train acc, test acc | 0.91815, 0.9193 train acc, test acc | 0.92345, 0.9253 train acc, test acc | 0.9260833333333334, 0.9282
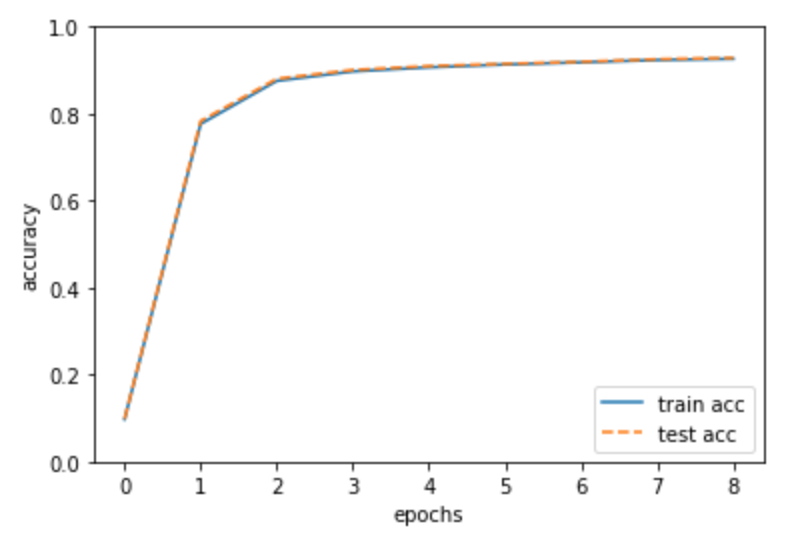
このようになりました。
少し補足すると、今回のiter_per_epochは600となっています。(60000 / 100)
そのため、グラフも8エポックまで(ループ回数5000 / 600 ≒ 8)がx軸となっています。
そして、エポックが進むにつれて、認識精度が工場していることが分かると思います。
また、訓練データとテストデータを使って評価した認識精度は両方向上しており、2つの認識精度には差がほどんとないため、過学習も起きていないことが分かります。
ここまでニューラルネットワークを学習してきましたが、
5月から機械学習を勉強し始めて、約1ヶ月弱が経ちました。
過去に学んだものが点と点で繋がりだしているのを少しずつ感じてきてる、今日この頃です。
AIエンジニアになるため、頑張ります。