こんばんは。
本日はPythonの演習ということで、素数列挙プログラムを作成しました。
ソース
私が作成したソースです。
おそらくちゃんと動きます。
import math # 素数判定関数 def isPrime(num): # 2未満の数字は素数ではない if num < 2: return False # 2は素数 elif num == 2: return True # 偶数は素数ではない elif num % 2 == 0: return False # 3 ~ numまでループし、途中で割り切れる数があるか検索 # 途中で割り切れる場合は素数ではない for i in range(3, math.floor(math.sqrt(num))+1, 2): if num % i == 0: return False # 素数 return True # 素数判定 def callIsPrime(input_num=1000): numbers = [] # ループしながら素数を検索する for i in range(1, input_num): if isPrime(i): numbers.append(i) # 素数配列を返す return numbers # 関数の呼び出し print(callIsPrime(1000))
出力はこんな感じです。
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
解説
少しだけ解説を。
素数判定では、
「合成数xはp≦√xを満たす素因子pをもつ」
という性質を利用することができます。
これはどういうことかといいますと、
「合成数xはp≦√xを満たす素因子pをもつ」=「xが合成数ならば、√x以下の約数を持つ」
と言うことです。
つまり、その数のルートをとってあげた数 以下の約数を持つということです。
なのでループの終了条件がmath.floor(math.sqrt(num))+1までになっている訳です。
単純にnumまで剰余演算をするのに比べると、ループ回数が減って処理速度が大幅に短縮されます。
あと高速化のため、偶数の場合は即Falseをリターンしたり、ループのステップ数を2にしたりしています。
ちなみに、callIsPrimeの引数を10, 100, 1000, 10000と増やしていったときに、どの程度処理時間が増加するか、グラフにしてみました。
処理時間の計測方法は、
%%timeit
# -- ここに計測したい処理 --
とすることで、計測できたりします。
%matplotlib inline import matplotlib.pyplot as plt max_vals= [1, 2, 3, 4] # 10, 100, 1000, 10000 のときにかかった時間をリストとして設定 times = [347*1e-6, 350*1e-6, 995*1e-6, 8.91*1e-3] plt.plot(max_vals, times)
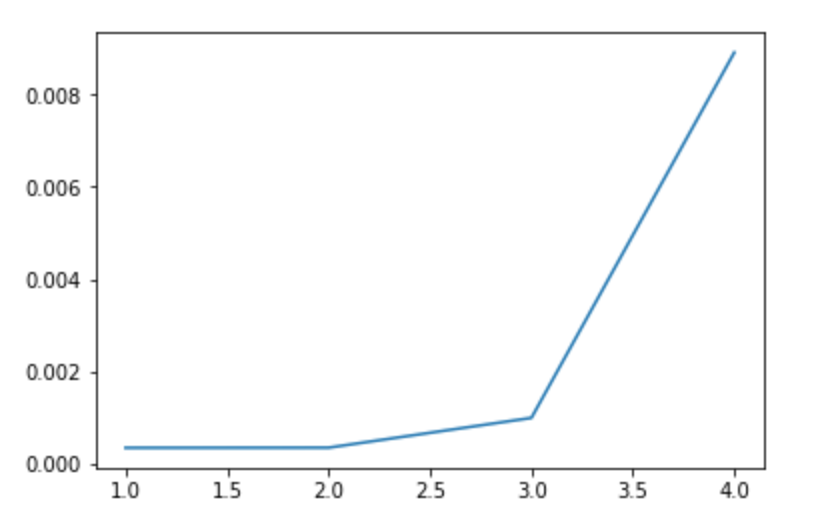
1000 → 10000にしたときに、処理時間は4倍になっていることが分かりますね。
まぁ、2ms → 8msの増加なので許容範囲でしょう。(汗)
Pythonでのコーディングも徐々に慣れてきました~
今日はこの辺りで。