こんにちは。takapy(@takapy0210)です。
本記事は、転職カウントダウンカレンダー 6日目の記事です。
はじめに
ランダムフォレストは機械学習を勉強したことのある人であれば一度は見聞きしたことのある手法でしょう。
回帰でもクラス分類でもランダムフォレストが広く使われており、多くの場合パラメータチューニングをせずに使えるし、データのスケール変換も必要ないので、とても手軽に使うことができます。
名前からも想像できるように、ランダムフォレストとはいくつもの異なる決定木を作りそれらをアンサンブルして予測するモデルです。
「いくつもの異なる決定木とは、具体的にどうやって生成しているのか」それをまとめた記事です。
ランダムフォレストとは
繰り返しになりますが、ランダムフォレストとは、決定木の問題点であった「訓練データに対する過剰適合」に対応する方法の1つであり、少しずつ異なる決定木をたくさん集めたものでアンサンブル学習します。
ランダムフォレストは個々の決定木は比較的うまく予測できているが、一部のデータに対して過剰適合してしまっているという考えに基づいています。それぞれ異なった方向に過剰適合した決定木をたくさん作れば、その結果の平均を取ることで過剰適合の度合いを減らすことができる、という訳です。
この戦略を実装にするには、たくさんの決定木を作成するだけでなく、個々の決定木はある程度ターゲットを予測でき、かつお互いに違っていなければなりません。
このお互い違うという部分を実現するために、決定木の構築過程で乱数を導入しています。
この乱数の導入方法には以下の2つがあります。
ブーストラップサンプリング(決定木を作るためのデータを選択する方法)
特徴量選択(分岐テストに用いる特徴を選択する方法)
この2点について解説した後に、pythonで実装してみます。
異なる決定木を作るための2つの乱数選択
以下に説明する「ブーストラップサンプリング」と「特徴量選択」により、ランダムフォレスト中の決定木が、それぞれ異なるものになります。
ブーストラップサンプリング
ランダムフォレストが決定木を作るときに、まずデータからブーストラップサンプリングと呼ばれる手法でデータを抽出を行います。
これは、n_samples個のデータから重複を許可した状態でデータをランダムにn_samples回選択するという手法です。(復元抽出)これによって、もとのデータセットと同じ大きさだが、データの一部(だいたい3分の1)が欠け、一部が何度か現れるデータセットを得ることができます。
例えば、リスト['a', 'b', 'c', 'd']からブーストラップサンプリングしてみると、['b', 'd', 'd', 'c']や['d', 'a', 'd', 'a']などを得ることができます。ここで得ることのできた新しいデータセットで決定木を作っていきます。
また、次に説明するように、決定木を作るアルゴリズムも少しだけ変更しています。
特徴量選択
通常の決定木の個々のノードは全ての特徴量を用いて最適なテストを選んで作成されています。しかし、ランダムフォレストが作る決定木は最適なテストを選ぶのではなく、特徴量のサブセットをランダムに選択し、その特徴量を使うものの中から最適なテストを選びます。これはパラメータmax_featuresで指定することができます。
例えば、max_featuresの値に元々の特徴量と同じ数値を設定すると、特徴量選択時の乱数生は無くなります。max_featuresを1に設定すると、分岐時に使う特徴量選択にはまったく選択肢がないことになります。
したがって、max_featuresを大きくするとランダムフォレスト中の決定木が似たようなものになり、max_featuresを小さくするとランダムフォレスト中の決定木は相互に大幅に異なるものになります。
この特徴量選択によって、決定木の個々のノードが異なる特徴量のサブセットを使って決定を行うようになります。
簡単に図で説明
例えば下記のようなデータセットを想定し、性別のクラス分類をしたいと想定します。
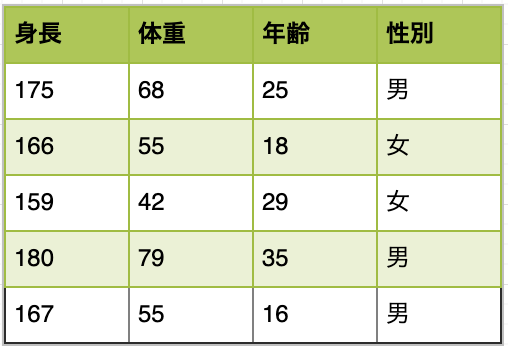
ブーストラップサンプリングでは、生成する決定木の数だけ下記のように新しいデータセットを生成します。
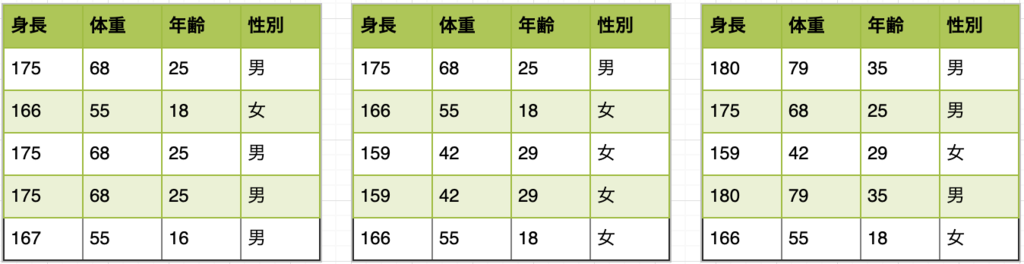
特徴量選択では、ある決定木のあるノードを生成する際に使う特徴量を限定します。元々あった特徴量は身長、体重、年齢でしたが、下記は、それぞれの決定木のそれぞれのノードを生成する際に使用する特徴量をランダムで2つ選択した例です。
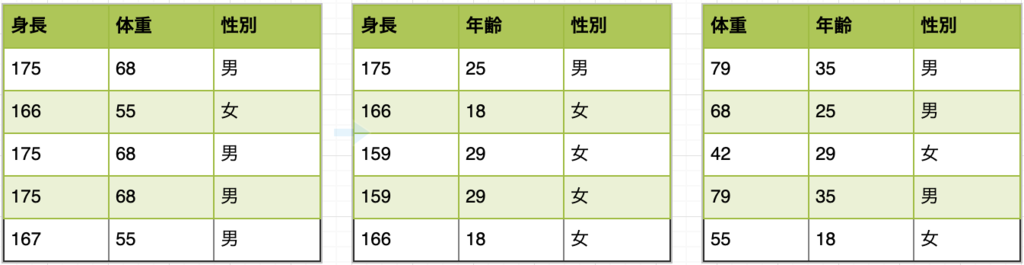
pythonで実装&可視化
make_moonsデータセットを用いてランダムフォレストモデルを生成し、どのようなクラス分類しているかを可視化してみます。
# ライブラリのインポート from sklearn.ensemble import RandomForestClassifier from sklearn.datasets import make_moons import numpy as np import matplotlib.pyplot as plt import pandas as pd import mglearn X, y = make_moons(n_samples=100, noise=0.25, random_state=3) # プロット plt.figure(figsize=(12,8)) mglearn.discrete_scatter(X[:,0], X[:, 1], y) plt.legend(loc='best') plt.gca().set_aspect('equal') plt.xlabel('X_1') plt.ylabel('X_2')
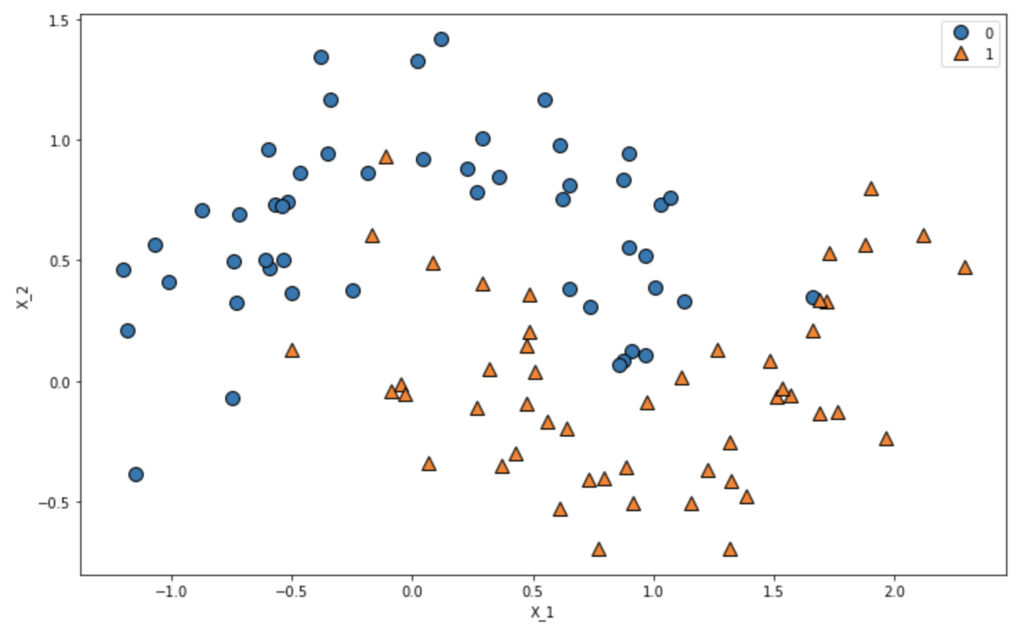
# データの分割 X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42) # モデル生成(決定木の数は5とする) forest = RandomForestClassifier(n_estimators=5, random_state=2019) forest.fit(X_train, y_train) # 個々の決定木を可視化してみる fig, axes = plt.subplots(2, 3, figsize=(20, 10)) for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)): ax.set_title("Tree {}".format(i)) mglearn.plots.plot_tree_partition(X_train, y_train, tree, ax=ax) mglearn.plots.plot_2d_separator(forest, X_train, fill=True, ax=axes[-1, -1], alpha=.4) axes[-1, -1].set_title("Random Forest") mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
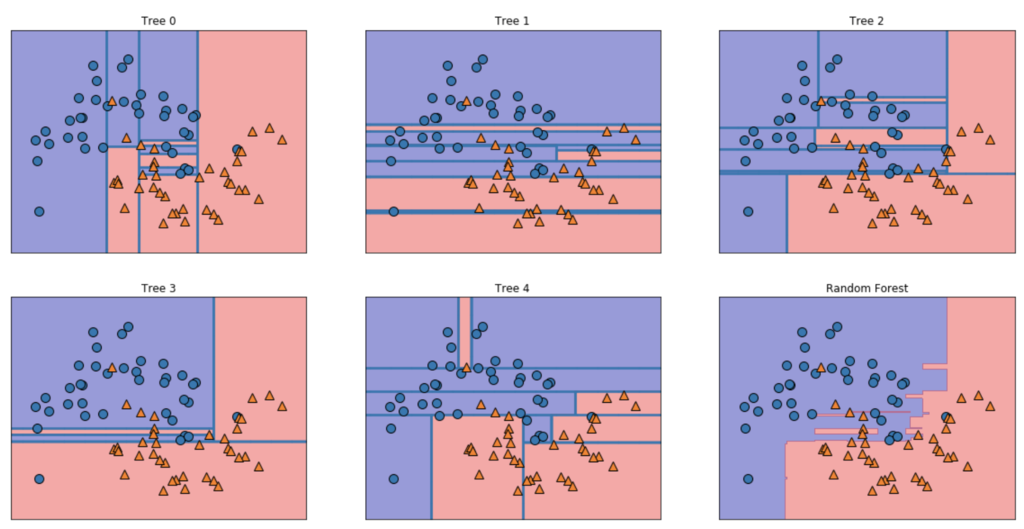
決定木の数を増やすと、境界線も滑らかになることが分かります。
# モデル生成(決定木の数を8とする) forest = RandomForestClassifier(n_estimators=8, random_state=2019) forest.fit(X_train, y_train) # 個々の決定木を可視化してみる fig, axes = plt.subplots(3, 3, figsize=(20, 15)) for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)): ax.set_title("Tree {}".format(i)) mglearn.plots.plot_tree_partition(X_train, y_train, tree, ax=ax) mglearn.plots.plot_2d_separator(forest, X_train, fill=True, ax=axes[-1, -1], alpha=.4) axes[-1, -1].set_title("Random Forest") mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)

最後に
上記でも見てきましたが、ランダムフォレストで優先して調整するべきパラメータとしては、n_estimators、max_features、max_depthなどの事前枝刈パラメータです。n_estimatorsは大きければ大きいほど良いとされていますが、大きくすることによる利益は徐々に減りますし、メモリの量も訓練にかかる時間も増大します。基準としては時間とメモリのある限り大きくするというものを設けておくと良いかもしれません。
また、max_featuresは基本的にはデフォルト値をそのまま使えば良い精度になる場合が多いです。追加でmax_leaf_nodesを追加すると性能が向上する可能性もあるため、その辺りはパラメータチューニングをやってみて決定していくと良いと思います。
以上