ギークなエンジニアを目指す男

機械学習系の知識を蓄えようとするブログ

トップ > Python > ゼロから作るDeepLearning 6章を学ぶ 〜重みの初期値について〜

ゼロから作るDeepLearning 6章を学ぶ 〜重みの初期値について〜

Python Python-機械学習 Python-機械学習-画像処理 Book

前回の続きです。
推奨されている重みの初期値について、まとめます。

taxa-program.hatenablog.com

重みの初期値を0にすることの危険性

正確には、重みを均一な値にすることはNGです。
なぜなら、誤差逆伝播法において、全ての重みの値が均一に更新されてしまうからです。
これでは、たくさんの重みを持つ意味がなくなってしまいますね。

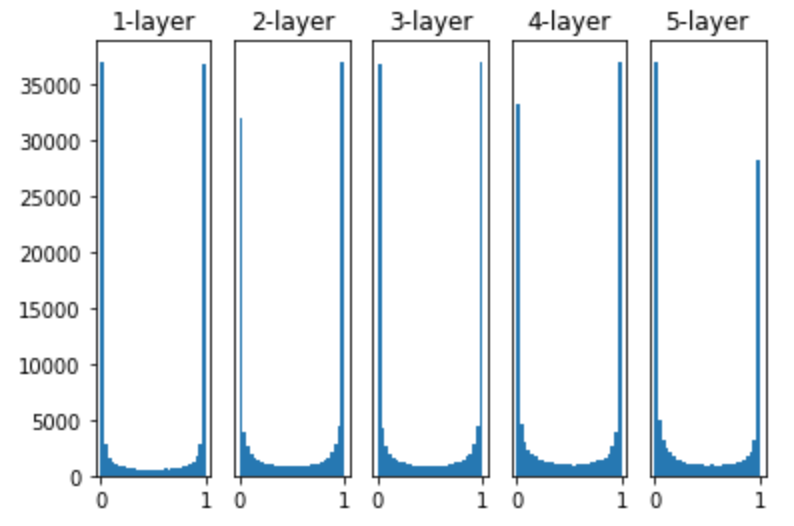
例えば、重みの初期値を、標準偏差が1のガウス分布を用いて5つの層をもつニューラルネットワークにダミーデータを渡して、隠れ層のアクティベーション（活性化関数の後の出力データ）を見てみます。
下記は活性化関数にsigmoid関数を使用していますが、各層のアクティベーションは0と1に偏っていることが分かります。

f:id:taxa_program:20180614214341p:plain

Xavierの初期値

Xavierの初期値とは、前層のノードの個数をnとした場合、\dfrac {1}{\sqrt {n}}の標準偏差を持つ分布を使用する、というものです。

Xavierの初期値を与えた場合のアクティベーションを見てみます。 f:id:taxa_program:20180614215621p:plain

上の層にいくにつれて、歪な形にはなっていますが、標準偏差が1のガウス分布を重みとした場合より、広がりがあることがわかると思います。

ReLU関数の場合の重み初期値〜Heの初期値〜

sigmoid関数やtanh関数は左右対称で中央付近が線形関数とみなせるため、Xavierの初期値が適していましたが、ReLU関数を用いる場合は、特化した初期値を用いることが推奨されています。
それがHeの初期値です。

Heの初期値は、前層のノードの数がn個の場合、\sqrt {\dfrac {2}{n}}を標準偏差とするガウス分布を用います。

ためしに、ReLU関数の「標準偏差0.01のガウス分布」、「Xavierの初期値」、「Heの初期値」でのアクティベーション分布を見てみましょう。

  • 標準偏差0.01のガウス分布

f:id:taxa_program:20180614221020p:plain

  • Xavierの初期値

f:id:taxa_program:20180614221043p:plain

  • Heの初期値

f:id:taxa_program:20180614221147p:plain

これを見ると、標準偏差0.01は論外、Xavierの初期値は層がディープになるにつれて、勾配損失が問題になってきそうなことが分かります。
一方でHeの初期値に関しては、層をディープにしても、分布の広がりが均一になっているため、逆伝播の際も適切な値が流れそうです。

まとめると

  • 活性化関数にReLUを用いる場合、Heの初期値
    \sqrt {\dfrac {2}{n}}
w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
  • 活性化関数にsigmoidやtanhを用いる場合、Xavierの初期値
    \dfrac {1}{\sqrt {n}}
w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)

を用いるのがベストプラクティスです。